Welcher Kabel-Querschnitt?
Zusammenfassung
Bei der Verdrahtung Im Inneren eines Gehäuses geht es primär um Übersichtlichkeit und kleine Biegeradien. Wie lassen sich Querschnittsflächen bzw. Durchmesser gerade bei strombelasteten Leitern klein halten, ohne dabei Gefahr zu laufen, dass die Kabel (zu) warm werden?
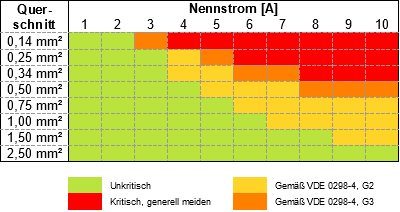Für Kabel bekannten Querschnitts, jedoch mit unbekannter (nicht spezifizierter) Strombelastbarkeit möchten wir die folgende Tabelle als Anhaltspunkt liefern, die in den darauffolgenden drei Abschnitten ausführlich hergeleitet wird.
Der Einsatz im grünen Bereich kann unter beliebigen Einbaubedingungen (allerdings bei üblicher Umgebungstemperatur) als unbedenklich eingestuft werden.
Der Einsatz in den angrenzenden beiden (gelben bzw. orangenen) Bereichen sollte jedoch nur unter den Bedingungen erfolgen (im wesentlichen eine Frage der Belüftung, der Kabelbündelung und der Umgebungstemperatur), die in der VDE 0298-4 etc. näher erläutert werden (siehe den nächsten Abschnitt).
Strombelastbarkeit nach VDE 0298-4
Die VDE-Richtlinien für die Strombelastbarkeit kupferner Leitungen (VDE 0298-4 sowie VDE 0891-1) unterscheiden inbezug auf die Art der Verlegung der Kabel drei Fälle:
- wärmeisoliert (z.B. in einem Rohr)
- in belüfteten Kanälen
- frei in der Luft
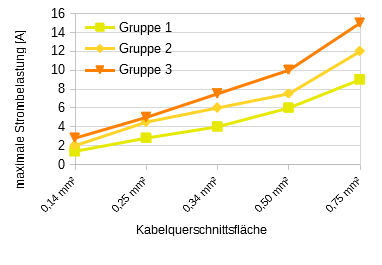Allerdings sinkt die jeweils angegebene Strombelastbarkeit a) im Falle der Bündelung von Kabeln und insbesondere b) infolge erhöhter Umgebungstemperatur noch einmal deutlich, und zwar um bis zu eine Größenordnung), was eine zuverlässige Bestimmung sehr aufwändig macht.
So liegt die Strombelastbarkeit einer Litze mit 0,14 mm² Querschnittsfläche laut Diagramm (rechts) zwischen 1,4 und 2,8 A. Der Distributor Reichelt gibt für seine entsprechenden Produkte jedoch 0,8 A als Grenzbelastung an, was auf eine entsprechend konservative Auslegung der Richtlinien schließen lässt.
Nun sorgt die Vorgabe für den einzuhaltenden maximalen Spannungsabfall („vom Keller zum Dach“) ohnehin für eher großzügig bemessene Kabelquerschnitte. Solche Vorgaben sind nun für das Gehäuseinnere wenig hilfreich, da ein solcher Spannungsabfall (z.B. 3%) über die vergleichsweise kurzen Distanzen innerhalb eines Gehäuses die Kabelisolierung zum Schmelzen bringen kann.
Rechenbeispiel: Verlustleistung im Gehäuseinneren bei (trügerisch kleinen) 3% Spannungsabfall
Statt des Spannungsabfalls soll deshalb im folgenden die Verlustleistung, die mit der Strombelastung des Leiters im Quadrat steigt, in den Mittelpunkt rücken, um den mindesterforderlichen Querschnitt aus einer zulässigen maximalen Verlustleitung abzuleiten.
Siehe dazu den nächsten Abschnitt.
Strombelastung und Verlustleistung
Die Verlustleistung P eines mit I bestromten Drahtes ergibt sich aus dem Produkt von I und dem mit der Bestromung verbundenen Spannungsabfall ΔU am Draht. Für den Spannungsabfall ΔU gilt folgende Beziehung (siehe https://electronicbase.net/), in die neben dem Strom I auch die Leitfähigkeit γ, die Länge l und die Querschnittsfläche A des bestromten Drahtes eingehen: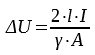
Für Kupferleitungen (γ = 58 · 10^6 S/m) mit 200 mm Länge (= maximale Drahtlänge innerhalb eines Boxtronik-Gehäuses der Baureihe 1016) ergibt sich die Verlustleistung P (in mW) für verschiedene Leitungsquerschnitte wie folgt:
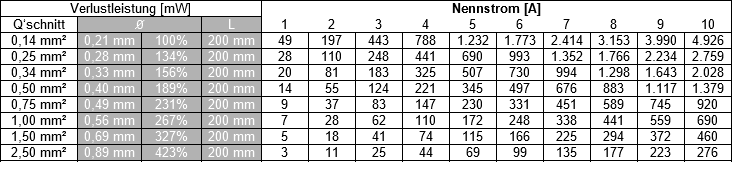
Verlustleistung eines Drahtes der Länge l = 20 cm in tausendstel Watt [mW].
Für jeden Leitungs-Querschnitt wäre jetzt – wie bei ohmschen Widerständen – eine Grenzleistung anzusetzen, unterhalb der ein dauerhaft unschädlicher Betrieb des Drahtes vorausgesetzt werden kann.
Dazu betrachten wir im nächsten Abschnitt die Grenzleistung von SMD-Widerständen unterschiedlicher Bauformen, um einen Anhaltspunkt zu bekommen, wieviel mehr Fläche ein Draht aufweisen muss, damit er sich bei derselben Verlustleistung nur um wenige Grad erwärmt.
Grenzbelastung
SMD Widerstände und ihre Grenzleistung
| Bauform | L | B | H | A | P | P/A |
| [zöllig] | [mm] | [mm] | [mm] | [mm²] | [mW] | [mW/mm²] |
| 0402 | 1 | 0,5 | 0,35 | 2,1 | 62,5 | 30 |
| 0603 | 1,6 | 0,8 | 0,45 | 4,7 | 100 | 21 |
| 0805 | 2 | 1,2 | 0,5 | 8,0 | 125 | 16 |
| 1206 | 3,2 | 1,6 | 0,6 | 16,0 | 250 | 16 |
| 1210 | 3,2 | 2,5 | 0,6 | 22,8 | 500 | 22 |
| 2512 | 6,3 | 3 | 0,55 | 48,0 | 1000 | 21 |
Im Sinne der eben durchgeführtern Betrachtung über die Größenverhältnisse der abstrahlenden Fläche eines heißen und eines gerade eben warmen Gegenstandes sollte ein Draht nicht mehr als 0,2 mW/mm² abstrahlen.
Eine Verlustleistung von 200 mW (2A @ 0,14 mm²) werden von SMD-Widerständen der Bauform 1206 (~ 16 mm² Oberfläche) gut verkraftet. 1.200 mW (7 A @ 0,14 mm²) bedürfen dagegen mindestens eines SMD-Widerstandes der Bauform 2512 (~ 48 mm² Oberfläche).
Die Grenztemperatur insbesondere von Hochlastwiderständen darf teilweise bei weit über 100 °C liegen. Um dieselbe Abstrahlungsleistung bei nur wenigen Grad über Umgebungstemperatur zu bekommen, muss die abstrahlende Oberfläche – je nach erlaubter Temperaturerhöhung – um den Faktor 30 bis 130 größer sein als die des SMD Widerstandes.
Verschieden temperierte Körper mit gleicher Strahlungsleistung
Die Strahlungsleistung P einer Oberfläche in Watt/m² verhält sich wie deren absolute Temperatur zur vierten Potenz (zweimal quadrieren, für eine korrekte Bilanz muss die von der Umgebung aufgenommene Strahlungsleistung abgezogen werden). Das Verhältnis dieser Strahlungsleistung P zweier Körper – einer bei 120 °C und einer bei wenigen °C über Umgebungstemperatur (0 °C) – gibt die folgende Tabelle wieder:
| Objekt | t [°C] | T [K] | PSMD/PDraht |
| SMD-Widerstand | 120 | 393 | – |
| Draht | 34 | 307 | 34 |
| Draht | 33 | 306 | 46 |
| Draht | 32 | 305 | 69 |
| Draht | 31 | 304 | 138 |
| Umgebung | 30 | 303 | – |
Darf der Draht beispielsweise 3 °C wärmer als seine Umgebung sein, dann muss er eine um den Faktor 34 größere Oberfläche als der SMD-Widerstand haben. Geht es um 200 mW, die ein SMD-Widerstand der Bauform 1206 (~ 16 mm² Oberfläche) dauerhaft abstrahlen kann, sollte der Draht also eine Oberfläche von mindestens 544 mm² haben. Die Oberfläche eines Drahts mit einer Länge von 200 mm und einer Querschnittsfläche von 0,14 mm² verfügt über 264 mm² Drahtoberfläche bzw. über 628 mm² Kabeloberfäche.
AWG - Umrechnungstabelle
| American Wire Gauge (AWG) | Querschnitt | metrisches Äquivalent |
| mm² | mm² | |
| 14 | 2,08 | 2,5 |
| 16 | 1,31 | 1,5 |
| 18 | 0,823 | 1 |
| 19-20 | 0,653 | 0,75 |
| 21 | 0,41 | 0,5 |
| 22 | 0,326 | 0,34 |
| 24 | 0,205 | 0,25 |
| 26 | 0,129 | 0,14 |
| 28 | 0,081 | 0,09 |